EMOF et la syntaxe abstraite du Canevas de l’empathie (partie 1)

Pour Osterwalder et al. (2014), les entrepreneurs qui réussissent sont ceux qui prennent à cœur les buts, les problèmes et les attentes des clients. Cette conviction les a poussés à créer le Canevas de l’empathie (Osterwalder et al., 2014, pp. 10–25), un langage de modélisation qui nous invite à approfondir la connaissance de nos clients afin de leur proposer naturellement des produits et des services qui leur plairont.

Ce langage, nous l’avons testé, et nous l’avons trouvé tellement génial que nous avons résolu d’en faire un logiciel.

Mais avant de coder quoi que ce soit, la première étape est de détailler le plus explicitement possible les concepts que nous pouvons modéliser avec le Canevas de l’empathie, et qu’il va falloir que nous demandions à l’ordinateur de représenter symboliquement sur l’écran. Pour faire cela, nous allons recourir à un langage spécialisé dénommé EMOF (Object Management Group, 2016, pp. 25–34). Car EMOF privilégie la précision, là où le français et les autres langues naturelles favorisent les sous-entendus et compliquent par conséquent la programmation.

Comment modéliser avec EMOF

Les concepts sont des catégories — des classes, comme les appellent les informaticiens — dans lesquelles on range des choses qui, malgré leur identité propre, partagent des propriétés communes. L’auteur de ce billet est un exemple — une instance (tel est le terme technique) — du concept de Blogueur, parce qu’il présente la caractéristique principale d’un Blogueur : il publie régulièrement du Contenu sur un Blogue, qui est, en quelque sorte, son Espace personnel de communication sur l’internet.

Quand nous mettons la majuscule à un nom commun ou à une locution nominale, par exemple à Blogueur, Contenu, Blogue ou Espace de communication, nous indiquons que c’est en tant que concept qu’il nous intéresse. En EMOF, cela se fait savoir en plaçant ledit nom commun ou ladite locution nominale à l’intérieur d’un rectangle (figure 1).

Si un concept a un nombre fini et raisonnable d’instances, et si nous les connaissons toutes, nous pouvons les lister en dessous de son nom, en prenant soin de faire précéder celui-ci de la mention «énumération» (figure 1). Lundi, mardi, mercredi, jeudi, vendredi, samedi et dimanche sont, par exemple, les seules instances du concept de Jour (figure 1).

Tout à l’heure, nous avons défini le concept de Blogueur en l’associant à celui de Contenu et celui de Blogue par la relation « publie sur ». Puis nous avons associé le concept de Blogue à celui d’Espace de communication par la relation « est un ».

C’est exactement de cette façon que l’on s’exprime en EMOF : on décrit des concepts à l’aide d’autres concepts, que l’on relie à nouveau à d’autres concepts, et ainsi de suite jusqu’à ce qu’il ne reste plus que des concepts primitifs, c.-à-d. jugés suffisamment simples et élémentaires pour être compris par ceux qui nous liront.

Graphiquement, pour montrer que deux concepts sont liés, on trace une ligne qui touche le pourtour des rectangles qui les représentent (figure 2). Sur cette ligne, il est obligatoire de préciser à côté de chaque concept son rôle et sa cardinalité dans la relation (figure 2).

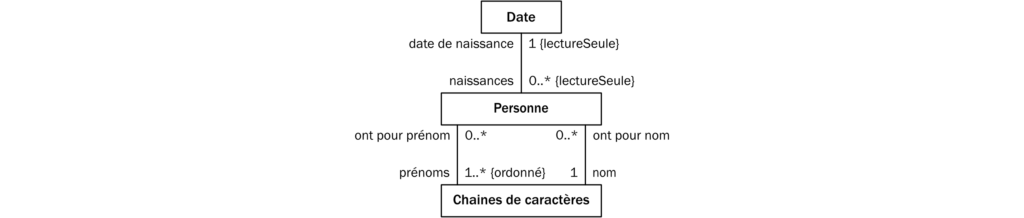
Sur la figure 2, nous avons introduit les concepts de Date, de Personne et de Chaîne de caractères. Ce dernier est l’appellation par laquelle les informaticiens désignent du texte brut comme, par exemple, "repos", "un paysage magnifique", ou "j'aime les méthodes formelles". L’usage veut que l’on signale le début et la fin d’une Chaîne de caractères avec « " » — à ne pas confondre avec les guillemets anglais « “ » et « ” ».

La figure 2 montre trois relations :

1. Une relation entre les Personnes et les Chaînes de caractères dans laquelle les Chaînes de caractères jouent le rôle de noms de famille. La cardinalité égale à 1 du côté des Chaînes de caractères dit qu’une Personne a au moins un et un seul nom, tandis que la cardinalité 0..* du côté des Personnes dit qu’une Chaîne de caractères est le nom de zéro ou plusieurs Personnes. En France, il y a par exemple beaucoup de "Dupont" mais aucun "Azerty".
2. Une relation entre les Personnes et les Chaînes de caractères dans laquelle les Chaînes de caractères jouent le rôle de prénoms. La cardinalité égale à 1..*{ordonné} du côté des Chaînes de caractères dit qu’une Personne a au moins un ou plusieurs prénoms, et que les notions de premier prénom, deuxième prénom, troisième prénom, etc., sont importantes, tandis que la cardinalité 0..* du côté des Personnes dit qu’une Chaîne de caractères est un des prénoms de zéro ou plusieurs Personnes.
3. Une relation entre les Personnes et les Dates dans laquelle les Dates jouent le rôle de dates de naissance. La cardinalité égale à 1 du côté des Dates dit qu’une Personne a au moins une et une seule date de naissance, tandis que la cardinalité 0..* du côté des Personnes dit qu’à une Date donnée naissent zéro ou plusieurs Personnes. Les « {lectureSeule} » visibles sur le modèle ne font pas partie des cardinalités. Nous allons expliquer leur signification dans un instant.

En termes généraux, dans une relation entre deux concepts C et D, la cardinalité de C est de la forme n..pQ, où n et p sont respectivement les nombres minimum et maximum d’instances de C avec lesquelles une instance de D peut être liée. Il va de soi que p doit être supérieur ou égal à n. La notation n..* signifie que p est sans limite (mais pas infini). EMOF nous autorise à écrire directement n au lieu de n..n, et * plutôt que 0..*.

La partie Q est optionnelle. Il s’agit des compléments « ordonné » et « nonUnique » à ajouter entre accolades si besoin. L’« ordonné » s’emploie lorsqu’il y a un premier, un second, un troisième, etc., et que le nombre ordinal d’une instance est une information indispensable. Nous avons vu son utilité sur la figure 2. Pour comprendre le « nonUnique », il faut savoir que, par défaut, une relation ne connecte jamais deux instances plusieurs fois. Le modèle de la figure 2 dit implicitement que chacun des prénoms d’une Personne est différent.

Cette propriété des relations s’avère parfois limitante. Par exemple, sur la figure 3, les Internautes du modèle de gauche ne consultent jamais deux fois la même Page web. Ce modèle est évidemment irréaliste. À droite, nous l’avons corrigé en complétant la cardinalité 0..* du côté des Pages web par « {ordonné, nonUnique} ». L’« ordonné » souligne que les visites d’un Internaute ont une chronologie, et le « nonUnique » modélise sa liberté de revenir sur une Page web autant de fois qu’il le souhaite. Nous n’avons pas mis d’« ordonné » du côté des Internautes ; nous pensons qu’un « nonUnique » suffit car pour une Page web, ce qui compte est le nombre total de visites, indépendamment de l’ordre dans lequel elles ont lieu (c’est un point de vue discutable).

Les « ordonné » et « nonUnique » sont à prendre en considération uniquememt si la cardinalité est de la forme n..* ou n..p avec p ≥ 2.

Les relations évoluent généralement au cours du temps. Il se peut, par exemple, qu’une Personne change de nom ou de prénom suite à un mariage, pour s’intégrer dans une communauté, ou pour d’autres raisons personnelles. Les relations où chaque connexion entre instances demeure immuable une fois établie sont signalées par « {lectureSeule} ». C’est parce que nous savons que la date de naissance d’une Personne ne changera jamais que nous avons placé des « {lectureSeule} » à côté des naissances et des dates de naissance sur la figure 2.

Rien n’interdit de faire apparaître un concept plusieurs fois ou de le relier à lui-même. Les deux modèles de la figure 4 ci-dessous sont tout à fait corrects et expriment le fait qu’une Personne a deux parents et zéro ou plusieurs enfants.

Si, au niveau des instances, toutes les connexions formées par une relation sont déductibles à partir d’une ou de plusieurs autres relations déjà modélisées, alors elle est dérivée. L’âge d’une Personne et le Jour qui l’a vue naître sont deux exemples de relations — la première entre des Personnes et des Entiers, et la seconde entre des Personnes et des Jours (figure 5) — calculables ou retrouvables à partir de sa date de naissance. Sur un modèle, on reconnaît une relation dérivée à ce que les rôles donnés aux concepts qu’elle relie sont préfixés par « / » (figure 5).

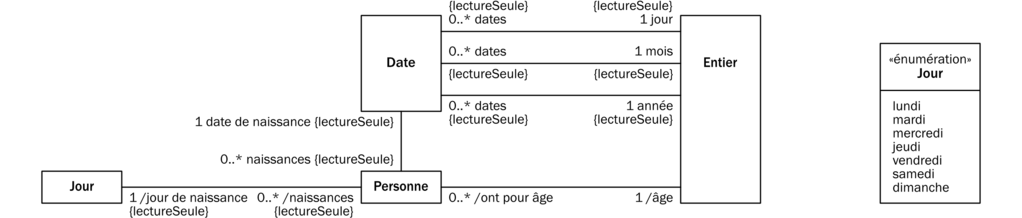
Les Dates sont souvent abrégées sous forme de triplets d’Entiers, avec un Entier pour l’année, un autre entre 1 et 12 pour le mois de l’année, et un autre entre 1 et 28, 29, 30 ou 31 pour le jour du mois. Par exemple, selon les pays, le 14 mai 2019 s’écrit aussi 14/05/2019, 05/14/2019 ou 2019/05/14. C’est cela que modélise les trois relations entre les Dates et les Entiers sur la figure 5.

Revenons maintenant à notre Blogueur. Nous avons débuté cette section en expliquant que la caractéristique principale d’un Blogueur est de publier régulièrement du Contenu sur un Blogue. Dans cette description, la relation « publier sur » fait intervenir trois concepts : celui de Blogueur, celui de Contenu et celui de Blogue. Or, en EMOF, les concepts ne se relient que deux par deux. Comment allons-nous donc modéliser cette relation ?

Il faut passer par un concept de liaison (figure 6).

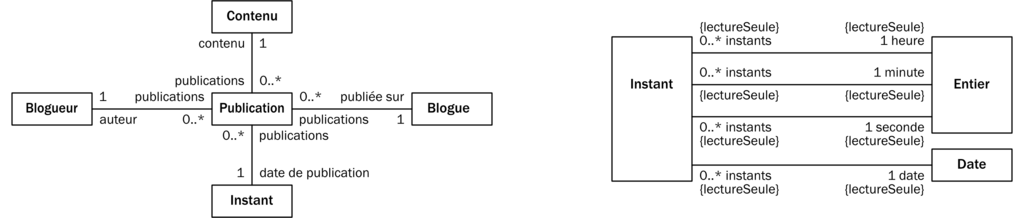
Sur la figure 6, le concept de Publication se charge de faire la liaison entre les Blogueurs, les Contenus et les Blogues. Nous en avons profité pour le lier à un quatrième concept, les Instants, afin de tenir compte de l’Instant où un Blogueur publie du Contenu sur son Blogue (figure 6). Un Instant est une Date complétée d’une précision de l’heure, de la minute et de la seconde (figure 6).

Deux Blogues ne peuvent pas avoir un même Contenu publié par le même Blogueur au même Instant. C’est impossible. De plus, si un Blogue devient inaccessible, par exemple en raison de sa suppression, il en sera de même pour toutes ses Publications. Ces deux propriétés de la relation entre les Publications et les Blogues font entrer les Publications dans la composition des Blogues. Sur un modèle, un losange noir doit être accolé au concept qui résulte de la composition (figure 7).

La définition exacte de la composition est la suivante. Une relation entre deux concepts C et D (dans l’exemple précédent, C était le concept de Blogue et D celui de Publication) est une composition si et seulement si :

1. aussi longtemps qu’une instance de C est connectée à une instance d de D, aucune autre instance de C ne peut être connectée à ce d (la cardinalité de C est donc forcément de 0..1 ou 1) ;
2. la perte ou l’inaccessibilité d’une instance c de C cause celle de toutes les instances de D connectées à c.

Pour un Blogueur, un Blogue est un Espace personnel de communication sur l’internet. Dire qu’un Blogue est un Espace de communication c’est dire que toute instance du concept de Blogue est aussi une instance du concept d’Espace de communication. Dans la terminologie d’EMOF, le concept de Blogue est une spécialisation du concept d’Espace de communication, et le concept d’Espace de communication est une généralisation du concept de Blogue. EMOF symbolise ce genre de relation par une flèche à tête creuse (figure 8) qui part de la spécialisation (les Blogues) vers la généralisation (les Espaces de communication). C’est le seul type de relation qui n’a ni rôles ni cardinalités (figure 8).

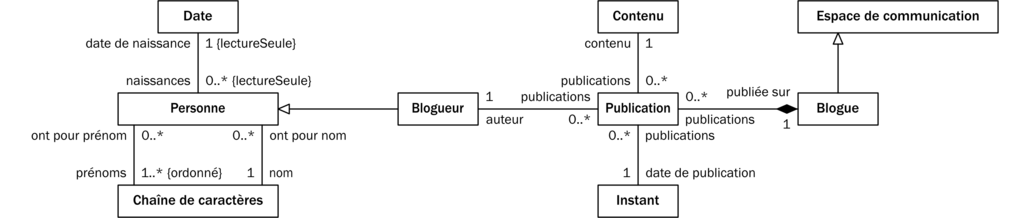
Une spécialisation hérite de toutes les relations du concept qu’elle spécialise. Par exemple, sur la figure 8, puisqu’un Blogueur est une Personne, il a, comme toute Personne, un nom, un ou plusieurs prénoms, et une date de naissance.

Bien ! Après ce tour d’horizon de la notation d’EMOF, nous sommes désormais équipés pour nous attaquer à la syntaxe abstraite du Canevas de l’empathie. Bien que nous n’ayons pas montré toutes les possibilités de modélisation que nous offre ce métalangage — cela aurait rendu cet article long et ennuyeux — ce que nous avons appris est suffisant pour commencer. Un peu de mise en pratique va nous faire du bien. Nous compléterons notre exposé au fur et à mesure des billets.

Une syntaxe abstraite pour le Canevas de l’empathie

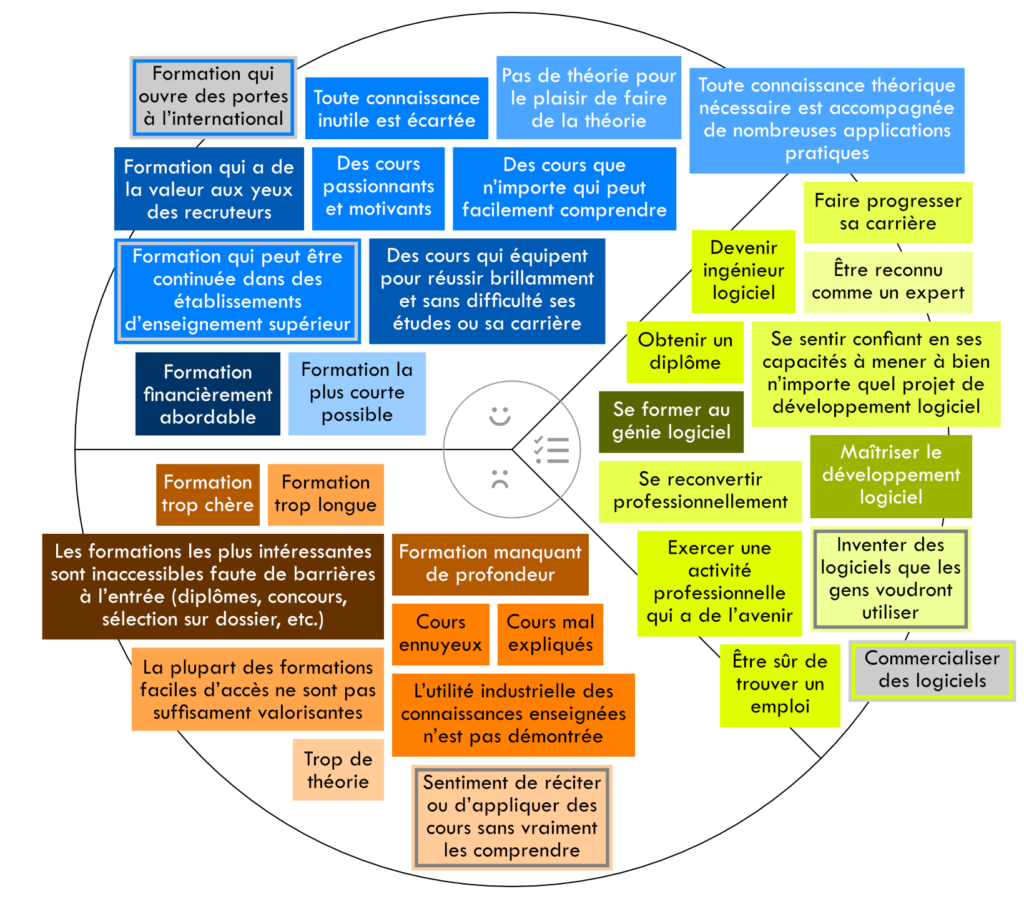
Pour rappel, un langage de modélisation est un ensemble de règles suivies par ses utilisateurs pour représenter et transmettre leurs idées autour d’un thème spécifique. Le Canevas de l’empathie (figure 9) est, par exemple, un langage de modélisation qui a pour thème la compréhension de ce que les clients d’une entreprise recherchent.

La syntaxe abstraite d’un langage de modélisation est l’inventaire des concepts à propos desquels il permet à ses utilisateurs de parler, et la liste des connexions entre ces concepts qu’ils ont, par lui, la possibilité d’exprimer. Ci-dessous, sur la figure 10, nous nous sommes servis d’EMOF pour présenter la syntaxe abstraite du Canevas de l’empathie.

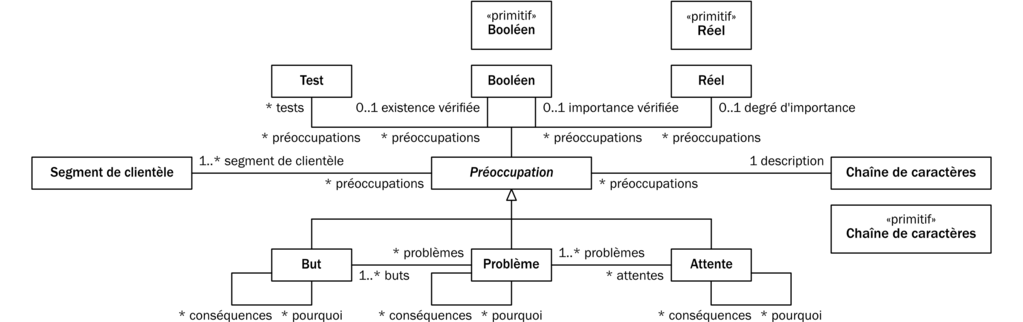
Nous sommes arrivés à cette syntaxe abstraite en faisant l’analyse suivante :

1. Le cercle en arrière-plan du Canevas de l’empathie (figure 9) symbolise un Segment de clientèle — ici, en l’occurrence, des lecteurs de cours de génie logiciel. Les Segments de clientèle sont donc des concepts de la syntaxe abstraite (figure 10).
2. Les zones de droite, du bas et du haut de ce cercle (figure 9) sont respectivement réservées aux Buts, aux Problèmes et aux Attentes du Segment de clientèle. Les Buts, les Problèmes et les Attentes sont donc, eux aussi, des concepts de la syntaxe abstraite (figure 10).
3. Tout But, Problème ou Attente d’un Segment de clientèle est pour lui une Préoccupation (figure 10). Sur la figure 10, « Préoccupation » est écrit en italique. En EMOF, cela signifie qu’il s’agit d’un concept abstrait, au sens où, contrairement aux Buts, aux Problèmes et aux attentes, il n’apparaît pas directement sur le Canevas de l’empathie (figure 9) ; il n’existe qu’indirectement au travers des instances de ses spécialisations que sont, justement, les Buts, les Problèmes et les Attentes (figure 10).
4. Chaque Préoccupation — chaque But, Problème ou Attente — est donnée sous la forme d’un texte descriptif (figure 9) qui est une Chaîne de caractères (figure 10).
5. Plus la couleur de fond d’une Préoccupation — d’un But, d’un Problème ou d’une Attente — est foncéeclaire (figure 9), plus son importance aux yeux du Segment de clientèle est grande. Pour nous, ces nuances de couleur sont en fait des figurations de Nombres réels compris entre 0 et 100 (figure 10). En mathématiques, les Nombres réels — pour faire court, nous les appelleront les Réels (figure 10) — sont les nombres avec lesquels nous mesurons les choses du monde réel.
6. L’emploi ou le non-emploi d’une couleur de fond grise (figure 9) pour une Préoccupation — un But, un Problème ou une Attente — modélise un Booléen (figure 10), c.-à-d. une information qui est soit vraie soit fausse ; en l’occurrence, la vérification (dans le cas d’un fond non gris) ou la non-vérification (dans le cas d’un fond gris) de l’existence de cette Préoccupation par le biais d’une expérimentation (figure 10).
7. L’emploi ou le non-emploi d’une couleur de bordure grise (figure 9) pour une Préoccupation — un But, un Problème ou une Attente — modélise lui aussi un Booléen (figure 10) : la vérification (dans le cas d’une bordure non grise) ou la non-vérification (dans le cas d’une bordure grise) de son degré d’importance avec une expérimentation (figure 10).
8. Quand une Préoccupation — un But, un Problème ou une Attente — a fait l’objet d’une ou de plusieurs expérimentations, ces dernières sont documentées dans une fiche de test (figure 11). La syntaxe abstraite de cette fiche de test se trouve sans difficulté (figure 12). Sur la figure 10, la relation entre le concept de Préoccupation et celui de Test reflète le lien entre une Préoccupation et les expérimentations qui ont vérifié son existence ou son importance.
9. Les clients ont des Problèmes qui les empêchent d’atteindre leurs Buts, mais seules les solutions qui correspondent à leurs Attentes auront leur faveur (figure 9). C’est la raison pour laquelle, sur la figure 10, nous avons relié les Buts avec les Problèmes (les Problèmes empêchent les clients d’atteindre leurs Buts), et les Problèmes avec les Attentes (les clients ont des Attentes précises qui déterminent les solutions qu’ils jugent acceptables pour leurs Problèmes).
10. Enfin, un But, un Problème ou une Attente peut en cacher un autre : le pourquoi — l’explication — d’un But, d’un Problème ou d’une Attente est souvent un autre But, un autre Problème ou une autre Attente. Par exemple, sur la figure 9, le désir de se former au génie logiciel est peut-être motivé par l’envie de se reconvertir professionnellement afin, peut-être, d’exercer une activité qui a de l’avenir. Dans la syntaxe abstraite (figure 10), nous avons tenu compte de cette possibilité de liens causaux en ajoutant des relations connectant des Buts avec d’autres Buts, des Problèmes avec d’autres Problèmes, et des Attentes avec d’autres Attentes.

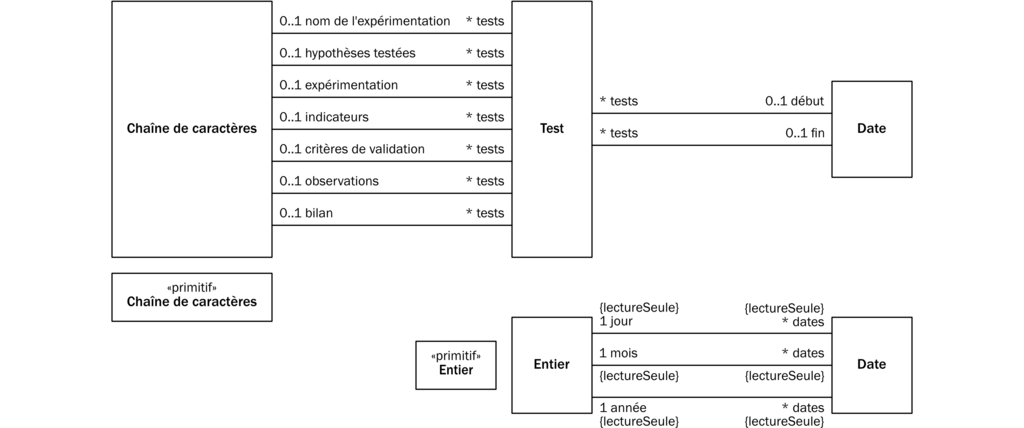
Comme on peut le voir, en EMOF on décrit des concepts à l’aide d’autres concepts, que l’on relie à nouveau à d’autres concepts, et ainsi de suite jusqu’à ce qu’il ne reste plus que des concepts primitifs jugés suffisamment simples et élémentaires pour être compris par ceux qui nous liront. La mention «primitif» sert à marquer les concepts que nous considérons primitifs. Ici, nous avons choisi les Booléens, les Entiers, les Réels et les Chaînes de caractères (figures 10 et 12).

Cette sélection est appropriée pour des modèles destinés à être relus par des personnes car, après de brèves explications, tout le monde peut se faire une idée de ce que sont les Booléens, les Entiers, les Réels et les Chaînes de caractères.

Le problème est que nos modèles s’adressent à l’ordinateur. C’est lui qui a besoin qu’on lui détaille les concepts que l’on retrouve dans le Canevas de l’empathie — les Segments de clientèle, les Buts, les Problèmes, les Attentes, etc. — afin d’être ensuite en mesure de les représenter symboliquement sur l’écran. Vous savez peut-être déjà qu’un ordinateur ne connaît rien d’autre que les chiffres 0 et 1 — appelés chiffres binaires ou bits (mot-valise formé à partir de l’anglais binary digits). Comment pourrait-il donc savoir ce que sont les Booléens, les Entiers, les Réels et les Chaînes de caractères ? Gardons la réponse à cette question pour le prochain billet.

Questions

Chacun des symboles qui composent une Chaîne de caractères s’appelle un caractère. Le r, e, p, o et s de "repos" sont des instances du concept de Caractère. Les Caractères sont par conséquent plus primitifs que les Chaînes de caractères :

Qu’est-ce qui, selon vous, peut conduire à garder malgré tout les Chaînes de caractères comme concept primitif à la place ou à côté des Caractères ?

Bibliographie

Crédits photographiques